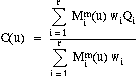Splines

A spline is a smoothed curve defined by input points and possibly by additional vector constraints. The spline curve and its derivatives are defined in the following illustration for a cubic spline segment.
 



 
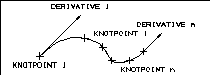
Figure Spline
 

 
There are many different types of spline curves. The ones used in NX are Non-Uniform Rational B-spline curves, sometimes referred to as "NURB" curves.
 
A Bezier curve is a B-spline curve that consists of only a single segment. A B-Spline curve is a multi-segment curve represented by a list of points called poles.
 
You can consider a spline curve as a list of Bezier curves, and a Bezier curve as a special type of B-spline curve.
 
See the functions in the uf_modl.h chapter.
 
Degree of a Spline
 
A Spline has a degree. Degree is a mathematical concept; it actually refers to the degree of the polynomial or rational functions used to describe the curve.
 
A higher degree curve is stiffer in the sense that you have to move its poles a long way to produce any appreciable change in the shape of the curve. Lower degree curves are more pliable, and tend to follow their poles much more closely.
 
In NX, the degree of a Spline must be between 1 and 24. However, we recommend the use of cubics (a degree of 3) when creating Splines. Creating lower degree curves results in faster performance during subsequent operations such as machining, display, etc. Using higher degree curves reduces the chance of transferring data to other systems which may not support them. Also, the creation of a high degree curve through many points may lead to unpredictable results.
 
Degree of a Spline
 
To create a Bezier, single segment curve, set the degree to one less than the number of points input.
 
B-Spline Curve Degree
 
For a B-spline curve, the degree is independent of the number of points. You select the desired degree knowing that the minimum number of points is one more than that degree.
 
points on curve
poles
 
Minimum/Maximum Number of Points
 
For a Bezier curve, the minimum number of points is two (minimum degree of 1) and the maximum number of points is 25 (maximum degree of 24 + 1). For a B-spline curve at least degree + 1 points must be specified.
 
Creation Options
 
The system interprets the specified points in one of two ways: as points through which the curve must pass; or as points defining the location of the poles.
 
Points on Curve
 
Allows you to define a list of points through which the curve will pass. The curve interpolates each specified point, as shown on Figure below. When you use this option, you have control over the curve in the sense that it will always pass through the points that you specify. However, take note that specifying a high degree curve using this option may produce unpredictable results.
 
Poles
 
Allows the system to interpret the specified points as poles of a control polygon. In general, these poles do not lie on the resulting curve, as shown in Figure below . Using the Poles option gives you much better control of the overall shape and character of the curve since the resulting curve follows the shape of the control polygon. Using Poles gives you a much better chance of avoiding unwanted undulations (reversals of curvature) in the curve.
 



 
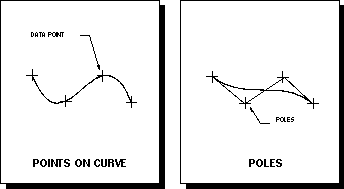
Figure Bezier: Points On Curve & Poles
 
Mathematical Composition of a Spline
 
A B-spline curve is a multi-segment polynomial curve represented by an array of points (called poles), a sequence of parameter values (called the Knot Sequence) and the degree of the curve.Let Pi (i = 1, 2,...,r) be the array of Poles defining the curve. Each Pole Pi is a four-dimensional object, which is composed of a 3D point,
 


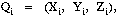
and a weight, wi,
 
where:
 



 
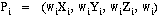
In the NX implementation, we require that the weights wi all be strictly positive.
 

 

 
Now suppose that the curve has degree m. Then the knot sequence will have r + m + 1 entries, which can be denoted by:
 



 
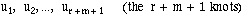
The knot sequence must be non-decreasing, i.e.
 



 
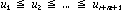
NX imposes restrictions on the knot sequence of a b-curve to ensure the curve is smooth.
 
most m.
 
In other words, we require:
 



 
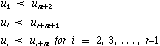
These restrictions guarantee that the curve is at least continuous in position. Discontinuities in the first derivative are not handled reliably by some NX applications. To minimize these types of discontinuities, we recommend that all b-curve knot sequences satisfy the stronger condition:
 



 
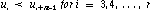
We also require a normalized knot sequence (scaled and shifted if necessary), so that:
 



 
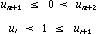
In most cases, it is advisable to make:
 



 
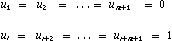
This will ensure that the curve starts at Q1 and ends at Qr , which makes it easier for the user to edit. However, these conditions are certainly not necessary.
 
Using the knots u1, u2,..., ur+m+1 we can construct r normalized B-spline basis functions of degree m, which we denote by

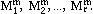
These basic functions are defined recursively, as follows:
 



 



 
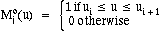
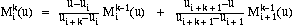
See References [1], [2] and [3] for further discussion of B-spline basis functions.
 
Then the equation of the curve is:
 



 
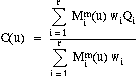
In fact, this curve is a non-uniform rational B-spline curve.
 
Several special cases are of interest:
 



 
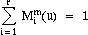
the equation of the curve reduces to:
 



 
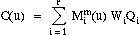
which is an ordinary (polynomial) B-spline curve.
 



 
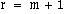
and if the knot sequence satisfy:
 



 
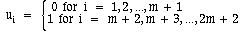
then the curve reduces to a single Bezier patch.
 


[1] Rogers and Adams
 
Mathematical Elements For Computer Graphics,
McGraw Hill, 1976
 
[2] Gerald Farin
 
Curves and Surfaces For Computer-Aided Geometric Design,
Academic Press, 1988
 
[3] de Boor
 
A Practical Guide To Splines
Springer-Verlag, 1978